IV) Diffuusiomenetelmät
Diffuusiomenetelmät ovat riippuvaisia epäpuhtausaineen lähteen olomuodosta. On olemassa kolme mahdollista lähtöaineiden olomuotoa, kun yritetään saada epäpuhtausaineita tarttumaan alustoihin, joita kutsutaan myös substraateiksi. Epäpuhtauslähteet voivat olla kaasumaisia, nestemäisiä tai kiinteitä aineita.

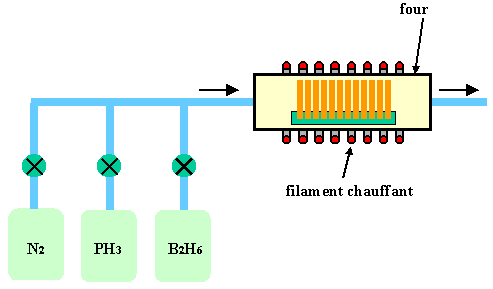
Kuva 23: Diffuusio uunissa kaasulähteistä. Neutraali kantajakaasu, kuten typpi, vetää mukaansa seostavat kaasut.
Kaasulähteitä ovat muun muassa arsiini, AsH3, fosfiini, PH3 ja diboraani B2H6 (kuva 23). On huomattava, että neutraali kantajakaasu kiertää jatkuvasti, jotta vältetään ympäröivästä kaasusta tulevien aineiden likaava vaikutus. Tämän typen täytyy olla hyvin puhdasta, jotta se ei vahingoita uunia.
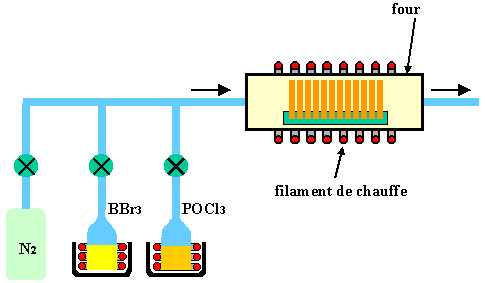
Kuva 24: Diffuusio nestelähteistä. Nesteupokkaita lämmitetään nesteen höyrystämiseksi, jotta se saadaan tunkeutumaan uuniin.
Vaikka kaasuja on helppo käyttää, ne ovat toisaalta erittäin vaarallisia, sillä muutaman ppm:n pitoisuus riittää tappamaan ihmisen. Sen vuoksi suositellaan nestelähteitä, kuten POCl3 tai BBr3, jotka ovat nestemäisiä huoneenlämmössä, mutta jotka on helppo höyrystää kuljetettavaksi diffuusiouuneihin (kuva 24).
Myös kiinteitä lähteitä voi käyttää. Sellaisia ovat lasit, jotka sisältävät jotain epäpuhtausainetta, kuten boorinitridiä tai lasi, joka on seostettu fosforiin. Näissä lähtöaineet ovat levyjen muodossa ja ne laitetaan uuniin lomittain seostettavien levyjen kanssa (kuva 25). Lasit höyrystyvät ja saostuvat levyjen päälle. Saostuksen jälkeen epäpuhtausaineet diffundoidaan alustan sisustaa kohti korkeassa lämpötilassa. Käytännössä saostunut lasi poistetaan ennen diffuusiota syövyttämällä, mikäli prosessin aikana alustalle siirtyneen epäpuhtausaineen määrä on riittävä.
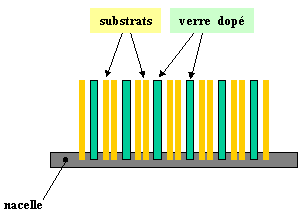
Kuva 25: Seostusmenetelmä kiinteistä lähteistä. Seostetut lasilevyt mahdollistavat kerrostuksen alustatelineeseen(kehtoon) kiinnitetyille substraateille.
Kaasulähteiden tapauksessa konsentraatio substraatin pinnalla on vakio, mikä merkitsee sitä, että kiinteässä olomuodossa konsentraatio pinnalla, Cs, on myös vakio. Reunaehto on siis:
C(0, t) = Cs (mielivaltaisella ajanhetkellä pisteessä x = 0)
Toinen ehto on alkuehto, jonka mukaan diffundoitavan aineen konsentraatio alustassa on alkuhetkellä nolla (tai merkityksetön). Tämä ehto on siis:
C(x,0) = 0 (mielivaltaisessa paikassa ajanhetkellä t =0)
Viimeinen ehto on intuitiviisempi. Äärettömän kaukana konsentraatio on nolla kaikilla ajanhetkillä. Tämä on hyvin ymmärrettävissä, jos muistaa sen, että diffuusion tapahtumiseksi gradientin on oltava nollasta eroava.
C( , t) = 0 (kaikilla ajanhetkillä)
, t) = 0 (kaikilla ajanhetkillä)
Näiden reunaehtojen perusteella differentiaaliyhtälön (Fickin 2. lain) ratkaisu on:
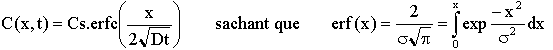
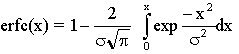
Kuvassa 26 on yhtälön graafinen esitys: käyrät piirretään yleensä puolilogaritmipaperille, jotta konsentraation vaihtelualue tulee hyvin esiin.
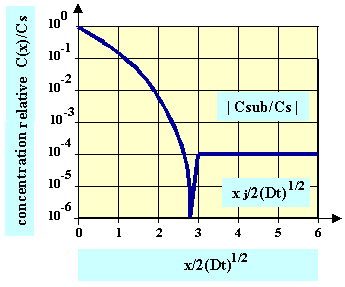
Kuva 26: Epäpuhtausaineen diffuusio vastakkaistyyppiseen hieman seostettuun alustaan, kun epäpuhtausainelähde on kaasu. Cs on pinnalla oleva konsentraatio.
VI) Diffuusio kiinteistä lähteistä tai pinnalla olevasta epäpuhtausannostuksesta:
Tarkastelu soveltuu myös tapaukseen, jossa epäpuhtausainetta törmäytetään puolijohteen pintaan ioni-istutuksella (tästä lisää myöhemmin). Kokonaismäärä (tai panos) on vakio.
C(x, 0) = 0 alkuehto
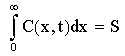
missä S on vakiosuuruinen.
Muistetaan että epäpuhtausaineen kokonaismäärä yksittäistä pintaa kohden on vakio. Lisäksi:
C(x,  ) = 0
) = 0
Differentiaaliyhtälön integrointi antaa tulokseksi yhtälön:
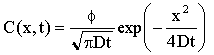
Saadun funktion muoto on gaussinen, kuten kuvasta 27 käy ilmi. Kun kokonaisannos on vakio, ja tapahtuu diffuusiota, maksimaalinen konsentraatio pienenee. Tämä tapahtuu termisen vaiheen jälkeen.
Valitse seostusparametrit (lämpötila, kesto ja epäpuhtausaineen laji) ja napsauta ”ok”, niin näet pitoisuusmuutokset käyriltä:
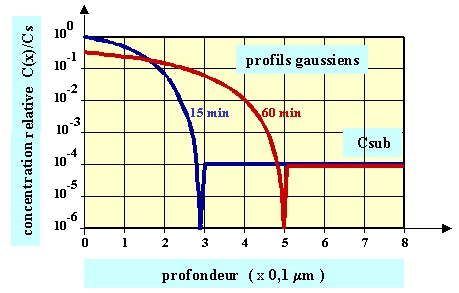
Kuva 27: Pinnalla olevasta annoksesta tapahtuvan diffuusion kehittyminen ajan muuttuessa. Käyrät ovat gaussisisia. Käyrän alla oleva integraali (lineaarisella asteikolla) on vakio.