IV) Procédés de diffusion
Les procédés de diffusion vont dépendre de la nature des sources de dopants. Il existe trois grands types de sources qui permettent de fournir les éléments dopants que l'on doit faire pénétrer dans les substrats. Ces sources sont gazeuses, liquides ou solides.

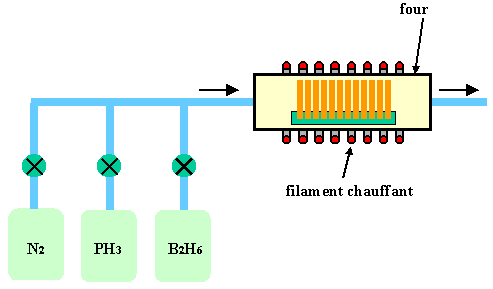
Figure 23 : Diffusion dans un four à partir de sources gazeuses. Les gaz dopants sont entraînés par un gaz porteur neutre, tel que l'azote.
Les sources gazeuses sont les gaz tels que l'Arsine, AsH3, la phosphine, PH3 ou le diborane B2H6 (figure 23). Notons qu'il circule en permanence un gaz neutre (azote) afin d'éviter toute pollution par des éléments venant de l'atmosphère ambiante. Cet azote doit être très pur afin de ne pas polluer le four.
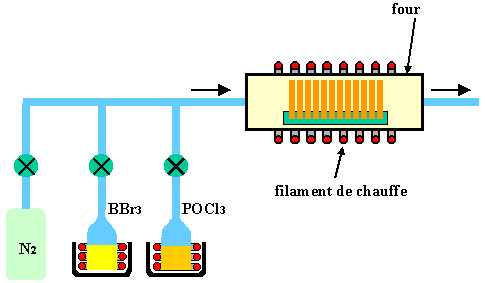
Figure 24 : Diffusion à partir de sources liquides. Les ballons contenant les liquides sont chauffés pour vaporiser le liquide afin de le faire pénétrer dans le four.
Bien qu'a priori ces gaz soient simples à mettre en œuvre, ils sont par contre très dangereux puisque létaux pour l'homme à quelques ppm de concentration. On leur préfère des sources liquides telles que POCl3 ou BBr3 qui sont liquides à température ambiante mais facilement vaporisées pour être introduites dans des fours de diffusion (figure 24).
On peut aussi utiliser des sources solides que sont les verres
contenant les dopants tels que nitrure de bore ou verre dopé au phosphore. Ces sources se
présentent sous forme de plaquettes et sont en général introduites dans le four en
alternance avec les plaquettes à doper (figure 25). Ces plaquaettes sont activées par une
oxydation qui permet de formet un oxyde. Dans le cas du Bore, du B
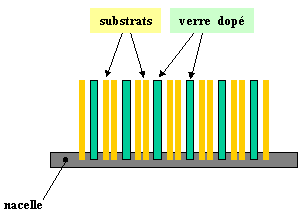
Figure 25 : Procédé de dopage à partir de sources solides. Les plaquettes de verre dopé permettent de réaliser un dépôt sur les substrats montés sur une nacelle (ou porte substrats).
V) Diffusion à partir de sources gazeuses :
Dans le cas des sources gazeuses, la concentration en surface dans le milieu ambiant est constante ce qui signifie qu'en phase solide, en surface la concentration, Cs, est aussi constante. La condition limite s'écrira donc :
C(0, t) = Cs (quel que soit le temps en x=0)
La deuxième condition est une condition initiale, qui suppose que la concentration de l'espèce à diffuser est initialement nulle (ou négligeable) dans le substrat. Cette condition s'écrit donc :
C(x, 0) = 0 (quel que soit x à t=0)
La dernière condition est plus intuitive. Elle postule qu'à une distance infinie, la concentration est nulle quel que soit le temps. Cela se conçoit bien si l'on se rappelle que pour que la diffusion se produise, il faut un gradient non nul de concentration.
C( , t) = 0 (quel que soit le temps)
, t) = 0 (quel que soit le temps)
A partir de ces conditions aux limites, la résolution de l'équation différentielle (2ème loi de Fick) donne :
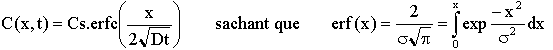
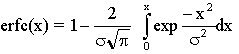
Une représentation graphique de ce profil est donnée figure 26 ; les courbes sont généralement tracées en échelle semi-logarithmique afin de bien apprécier le domaine de variation de concentration.
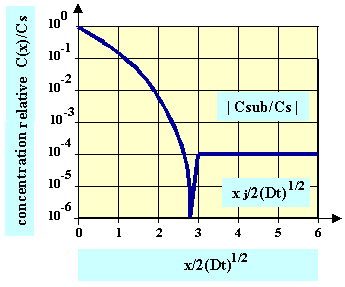
Figure 26 : Diffusion de dopant dans un substrat faiblement dopé de type opposé à partir d'une source de dopant gazeuse. Cs est la concentration en surface.
VI) Diffusion à partir de sources solides ou de dose en surface :
C'est aussi le cas lorsque le dopant a été introduit en surface par implantation ionique (voir plus loin). La quantité totale (ou dose) est constante.
C(x, 0) = 0 condition initiale
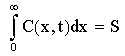
( S : dose totale constante)
Rappelons que la quantité totale de dopant par unité de surface (ou dose) est constante. De plus :
C(x,  ) = 0
) = 0
L'intégration de l'équation différentielle donne :
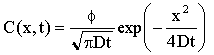
La forme du profil obtenu est gaussienne comme représentée sur la figure 27. Comme la dose totale est constante, lorsqu'il y a étalement, la concentration maximale diminue. C'est ce qui se produit après une étape à haute température.
Ajuster les paramètres de dopage (température, duréé et type de dopant) et cliquer sur "Ok" pour afficher les courbes:
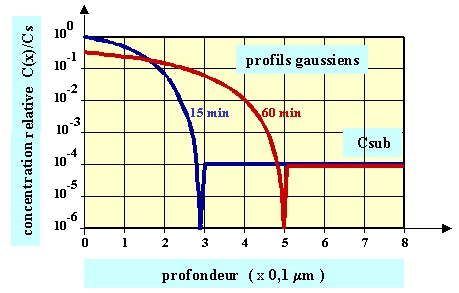
Figure 27 : Evolution du profil de dopage en fonction du temps pour une diffusion à partir d'une dose en surface. Les profils sont gaussiens. L'intégrale sous la courbe (en échelle linéaire) est constante.