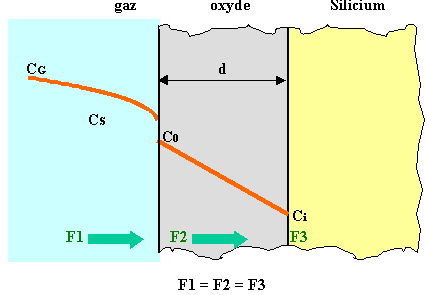
III) Modélisation de l'oxydation

Le modèle de base de l'oxydation est représenté sur la figure 40 qui distingue les 3 domaines dans lesquels il faut considérer des mécanismes différents :

- l'atmosphère ambiante contenant l'élément oxydant (soit de l'oxygène soit de la vapeur d'eau soit une combinaison de ces deux éléments,

- l'oxyde qui est traversé par l'élément oxydant par phénomène de diffusion. Notons que cette diffusion est négligeable à température ambiante mais fortement activée thermiquement,

- le Silicium, à la surface duquel se produit la réaction chimique d'oxydation.

Le calcul est basé sur l'analyse des flux de l'espèce oxydante dans les différentes zones. Si on raisonne en régime stationnaire, les trois flux sont égaux :

F1 = F2 = F3

Figure 40 : Modèle de base pour l'oxydation thermique. On met en oeuvre les 3 flux de l'espèce oxydante en phase gazeuse, dans l'oxyde et à l'interface Si/SiO2 (d'après B.E. Deal and A.S. Grove [9]).

F1 est le flux de l'élément oxydant en phase gazeuse. On a donc une équation de diffusion type 1ère loi de Fick. En appelant CG la concentration dans l'atmosphère, loin de la surface, et CS, la concentration en surface

F1 = hG (CG - CS)

hG est le coefficient de transfert de masse en phase gazeuse. On peut relier les concentrations CG et CS en fonction des pressions partielles en utilisant la loi des gaz parfaits :

CG =PG/kT CS =PS/kT

En utilisant la loi de Henry, on peut convertir la pression partielle en surface du cristal en une concentration équivalente à la surface mais du côté matériau solide.

CO = H.pS | C* = H.pG

H est la constante de Henry et C* est la concentration équivalente que l'on aurait dans le cristal pour une pression partielle dans le gaz. On peut ainsi écrire le flux F1 :

F1 = h (C* - Co)

h est le coefficient de transfert massique, avec

F2 est le flux de l'élément oxydant dans l'oxyde, qui obéit à la loi de Fick :

soit encore

F3 est le flux de réaction chimique à l'interface Si/SiO2. ce flux est proportionnel à la concentration de l'espèce oxydante au niveau de l'interface.

F3 = ks.Ci

A partir de la relation F1 = F2 = F3, on en déduit les coefficients Ci et Co :

A partir de ces équations, on peut maintenant évaluer la variation d'épaisseur d'oxyde, donc la croissance, à partir du flux F3. En appelant N1 le nombre d'atomes oxydants par unité de volume,

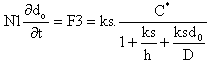
En supposant qu'au temps t = 0, l'épaisseur (initiale) de l'oxyde est di, la résolution de l'équation différentielle du premier ordre ci-dessus se fait simplement en passant le dénominateur du terme de droite au numérateur gauche. On obtient ainsi un élément en d_o et un élément constant à intégrer en dd_o. La solution se présente donc sous la forme :

d_o² + A.d_o = B (t + t)

avec

On peut alors exprimer l'épaisseur de l'oxyde, d_o, en fonction de A, B et t.

On peut simplifier l'expression de d_o en regardant des situations limites :

- pour des temps importants, l'épaisseur varie en racine du temps, c'est-à-dire que la croissance sera de plus en plus lente. Il faudra donc jouer sur la valeur de B en fonction de la température pour avoir des temps raisonnables d'oxydation (de quelques dizaines de minutes à quelques heures maximum).

t >> t

d_o² = B.t

- pour des temps faibles, l'épaisseur est proportionnelle au temps. La condition est la suivante :

(t + t) << A²/4B

d_o = (B/A).(t + t)

Les coefficients, A, B et t sont donnés dans les tableaux qui suivent (d'après B.E. Deal and A.S. Grove [9]). Ils dépendent du type de l'oxydation, sèche ou humide, et fortement de la température.

Constantes d'oxydation pour une oxydation humide du Silicium

Température d'oxydation °C	A (µm)	B(µm²/h)	B/A (µm/h)	t (heures)
1200	0,050	0,72	14,40	0
1100	0,110	0,510	4,64	0
1000	0,226	0,287	1,27	0
920	0,500	0,203	0,406	0

Constantes d'oxydation pour une oxydation sèche du Silicium

Température d'oxydation °C	A (µm)	B(µm²/h)	B/A (µm/h)	t (heures)
1200	0,040	0,045	1,12	0,0019
1100	0,090	0,027	0,30	0,00693
1000	0,165	0,0117	0,071	0,029
920	0,235	0,0049	0,0208	0,098
800	0,370	0,0011	0,0030	0,687
700	...	...	0,00026	7,81


		<= Cliquez sur OK pour afficher la courbe

Figure 41 : Variation de l'épaisseur d'oxyde en fonction de la durée d'oxydation pour une oxydation sèche effectuée à différentes températures (On tient compte de la présence de l'oxyde natif) et pour une oxydation humide.

Les coefficients intervenant dans ces tableaux varient très fortement en fonction de la température. Comme dans le cas de la diffusion d'atomes dopants dans le cristal, la diffusion des éléments oxydants dans l'oxyde sera thermiquement activée suivant une loi d'Arrhénius.

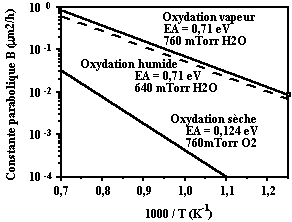
Figure 42 : Effet de la température sur le coefficient d'oxydation parabolique dans les cas d'oxydation sèche, humide et vapeur. La variation suit la loi d'Arrhénius (d'après B.E. Deal and A.S. Grove [9]).

Comme indiqué dans le modèle, pour des temps d'oxydation relativement faibles, la variation d'épaisseur en fonction du temps d'oxydation est pratiquement linéaire. Par ailleurs, pour des oxydations de faibles épaisseurs, on doit tenir compte de la présence de l'oxyde natif ce qui correspond à une ordonnée à l'origine non nulle sur la figure 43.

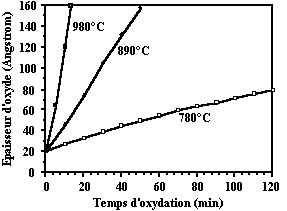
Figure 43 : Epaisseur d'oxyde obtenu par oxydation sèche à 780, 890 et 980 °C. La variation est pratiquement linéaire pour les faibles temps d'oxydation.

La réaction d'oxydation à l'interface tient compte du nombre d'atomes disponibles pour la réaction chimique. Lorsque les plans sont plus denses, la vitesse d'oxydation est légèrement supérieure. C'est le cas de l'oxydation d'un substrat orienté (111) comparé à celui orienté (100).

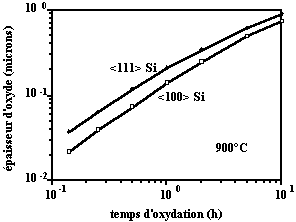
Figure 44 : Effet de l'orientation cristalline sur la croissance d'oxyde. Le substrat orienté <111> a une vitesse d'oxydation supérieure (d'après B.E. Deal [10]).